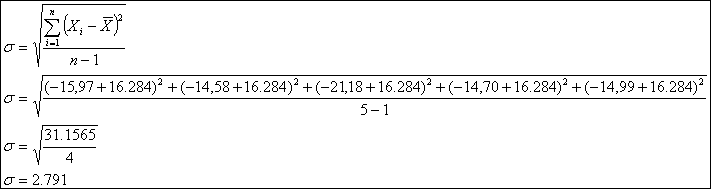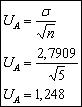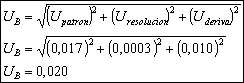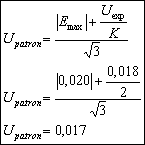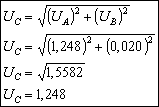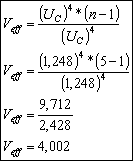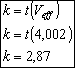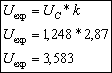<< Table of contents | Navigation:  Calibracion > Formulas Matemáticas

 

FORMULAS MATEMÁTICAS PARA ESTIMACIÓN DE LA INCERTIDUMBRE

 

 

●ESTIMACIÓN INCERTIDUMBRE TIPO A

 

La incertidumbre tipo A es la debida a la repetibilidad de los resultados de las mediciones del OBJETO DE PRUEBA, es una incertidumbre estadística  y se calcula mediante la desviación estándar, como sigue:

 

 

Donde:

 

-     () es la desviación estándar de la muestra

-     () es el número de mediciones realizadas en el punto

-     () Factor de cubrimiento en función de los grados de libertad para (n-1), cuando las mediciones sean ≤ 10, encontrando el valor de la t-student para un nivel de confianza del 68,27%, con lo cual se lleva los resultados a una distribución normal

 

oDesviación Estándar de la Muestra

 

Esta desviación se define como:

 

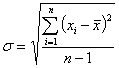
Donde:

 

-     () es el valor medido

-     () es el número de mediciones realizadas en el punto

-     () Media aritmética del total de las mediciones realizadas.

 

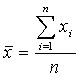
●ESTIMACIÓN INCERTIDUMBRE TIPO B

 

La incertidumbre tipo B es  la asociada al equipo de medición y esta compuesta por:

 

-     ()          Incertidumbre del Patrón

-     ()       Incertidumbre por Resolución

-     ()           Incertidumbre por Deriva

-     ()        Incertidumbre Por Objeto de Prueba

 

Su combinación, se realiza mediante la expansión de las incertidumbres y esta definida como sigue:

 

 

oIncertidumbre del Patrón

 

Es la debida al equipo de medición, se puede calcular de dos formas.

 

oEquipos Nuevos o Ajustados con Certificado de Calibración.

 

Se tiene en cuenta el máximo error más la incertidumbre expandida reportada, como sigue:

 

Donde:

 

-       () Error máximo reportado

-       () Incertidumbre expandida asociada al error máximo reportado

-       () Obedece a una distribución rectangular en la cual se asegura un resultado inferior al calculado en todo el rango

 

oEquipos Nuevos o Ajustados sin Certificado de Calibración.

 

Se tiene en cuenta las especificaciones dadas por el fabricante para el índice de clase o los límites de exactitud, como sigue:

 

 

Donde:

 

-       () Especificación del Fabricante

-       () Obedece a una distribución rectangular en la cual se asegura un resultado inferior al calculado en todo el rango

 

 

oIncertidumbre por Resolución

 

Se define como la máxima resolución de medición con la que se toman los datos medidos, como sigue:

 

 

Donde:

 

-       () Mínima lectura que se puede tener

-       (2) Obedece a una distribución cuadrática

 

oIncertidumbre por Deriva

 

Incertidumbre asociada a los cambios de las condiciones metrológicas del equipo patrón en el tiempo, se puede calcular de tres formas.

 

oAnálisis Metrológico.

 

Cuando se tienen datos históricos de la incertidumbre del Patrón, se toma como la máxima diferencia entre dos resultados continuos y se aplica una distribución rectangular, como sigue:

 

 

 

Se toma el mayor valor entre y , y es el que se tiene en cuenta para el cálculo.

 

Donde:

 

-       () Mayor valor entre y

-       () Obedece a una distribución rectangular en la cual se asegura un resultado inferior al calculado en todo el rango

 

 

oEquipos Nuevos o Ajustados con Certificado de Calibración.

 

Cuando no se cuenta con datos históricos, se toma la mayor incertidumbre expandida reportada en el certificado y se aplica una distribución rectangular, como sigue:

 

 

Donde:

 

-       () Máxima incertidumbre expandida reportada

-       () Obedece a una distribución rectangular en la cual se asegura un resultado inferior al calculado en todo el rango

 

oEquipos Nuevos o Ajustados sin Certificado de Calibración.

 

Cuando no se cuenta con datos históricos, y no se tiene certificado de calibración se toman las especificaciones dadas por el fabricante en estabilidad de Medición largo plazo, como sigue:

 

 

Donde:

 

-       () Estabilidad de Medición a largo plazo

 

oAporte de Incertidumbre Objeto de Prueba (OP)

 

Para la estimación del CMC, se debe tener en cuenta el rendimiento del mejor equipo existente que esté disponible, para una categoría específica de mediciones, se deberá incluir una cantidad razonable de contribución a la incertidumbre por la repetibilidad y contribuciones debidas a la reproducibilidad.

 

Donde:

 

-       () Exactitud del mejor objeto de prueba existente

 

●ESTIMACIÓN INCERTIDUMBRE EXPANDIDA

 

Incertidumbre reportada en el certificado de calibración, con un nivel de confianza del 95,45%; para estimarla se multiplica la incertidumbre combinada por un factor de cubrimiento (), definido por la distribución de la t-student para el nivel de confianza especificado, como sigue:

 

 

Donde:

 

-           () Incertidumbre Combinada, definida como la expansión de las incertidumbres tipo A y B:

 

-           () Factor de cubrimiento, para un nivel de confianza del 95,45% de la distribución t-student.

 

 

●Grados Efectivos de Libertad ().

 

Los grados efectivos de libertad se requieren para determinar el factor de cubrimiento () y se calculan mediante la formula de Welch-Satterhwaile, como sigue:

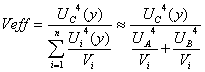
Donde:

 

-       () Incertidumbre Combinada

-       () Incertidumbre Tipo A

-       () Incertidumbre Tipo B

-       () Grados de Libertad de cada componente de incertidumbre. Para la incertidumbre tipo A de forma gaussiana, este valor es (n – 1)  y para la incertidumbre tipo B de forma rectángular, este valor es (). De acuerdo con esto la expresión para el cálculo de los grados efectivos de libertad, puede simplificarse de la siguiente manera:

 

 

 

 

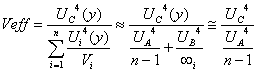
●REPORTE DE LA INCERTIDUMBRE DE MEDICIÓN.

 

La incertidumbre expandida () y el factor de cubrimiento ()  son reportadas en los certificados de calibración emitidos por el laboratorio de metrología, asociados al valor del error medido.

 

Ejemplo